2. Latent Gaussian Density Estimation¶
import jax.numpy as jnp
from jax import random
from melvin import LaplaceApproximation
import jax
import matplotlib.pylab as plt
from functools import partial
jax.config.update("jax_enable_x64", True)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
SEED = random.PRNGKey(220)
N_ROWS = 2000
LATENT_MEAN = 3.0
LATENT_STD = 1.0
NOISE_STD = 2.0
SEED, _seed_1, _seed_2 = random.split(SEED,3)
y_latent = jax.random.normal(key=_seed_1, shape=(N_ROWS,))*LATENT_STD + LATENT_MEAN
y = y_latent + jax.random.normal(key=_seed_2, shape=(N_ROWS,))*NOISE_STD
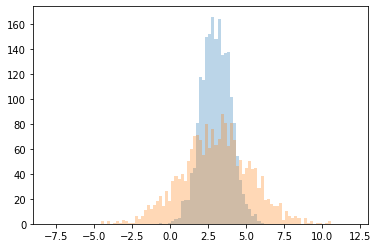
bins = jnp.linspace(-8,12,100)
plt.hist(y_latent, bins=bins, alpha=0.3)
plt.hist(y, bins=bins, alpha=0.3)
plt.show()
class GaussianDensityEstimator(LaplaceApproximation):
param_bounds = jnp.array([[jnp.nan, jnp.nan], [0, jnp.nan]])
def model(self, params, X):
mu = params[0]
std_latent = params[1]
std_noise = self.fixed_params[0]
std = jnp.sqrt(std_latent**2 + std_noise**2)
return jnp.array([mu, std])
def log_prior(self, params):
# Uninformative priors on both parameters
mu = params[0]
std_latent = params[1]
mu_log_prior = jax.scipy.stats.norm.logpdf(mu, loc=0.0, scale=100.0)
std_latent_log_prior = jax.scipy.stats.expon.logpdf(std_latent, scale=100.0)
return mu_log_prior + std_latent_log_prior
def log_likelihood(self, params, y, y_pred):
mu = y_pred[0]
std = y_pred[1]
log_like = jax.scipy.stats.norm.logpdf(y, loc=mu, scale=std)
return jnp.sum(log_like)
initial_params = jnp.array([5.0, 5.0])
gaussian_density_estimator = GaussianDensityEstimator(
name="Gaussian Density Estimator",
initial_params=initial_params,
fixed_params=jnp.array([NOISE_STD]),
y=y
)
print(gaussian_density_estimator)
/opt/hostedtoolcache/Python/3.9.5/x64/lib/python3.9/site-packages/scipy/optimize/_minimize.py:524: RuntimeWarning: Method BFGS does not use Hessian information (hess).
warn('Method %s does not use Hessian information (hess).' % method,
Laplace Approximation: Gaussian Density Estimator
Base distribution: normal
Fixed Parameters: [2.]
Fit converged successfully
Fitted Parameters:
[
3.024760513634774 +/- 0.04994854761415938,
0.9948447428567769 +/- 0.07930368410107927, [Lower Bound = 0.0]
]
MAP Posterior Prob = -4455.420834696258
SEED, _seed = random.split(SEED,2)
samples = gaussian_density_estimator.sample_params(prng_key = _seed, n_samples = 10000, verbose=True)
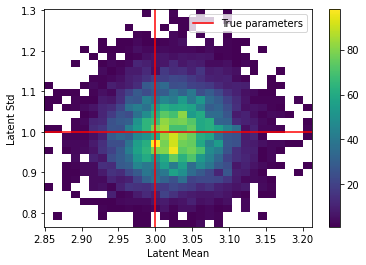
plt.hist2d(samples[:,0], samples[:,1], bins=(30,30), cmin=1)
plt.axhline(LATENT_STD, color="r", label="True parameters")
plt.axvline(LATENT_MEAN, color="r")
plt.xlabel("Latent Mean")
plt.ylabel("Latent Std")
plt.colorbar()
plt.legend()
plt.show()
Method = simple, Perf = -4459.114075145038
Method = importance, Perf = -4459.118794510243
**Best Method = simple**
SEED, _seed = random.split(SEED,2)
def get_pdf(params, x):
return jax.scipy.stats.norm.pdf(
x,
loc=params[0],
scale=params[1]
)
x = jnp.linspace(-3,10,100)
y_pdf = get_pdf(gaussian_density_estimator.params.x, x)
y_pdf_samples = gaussian_density_estimator.sample_params_map(
prng_key = _seed, n_samples = 300, func=get_pdf, args=(x,), verbose=True
)
y_pdf_low = jnp.percentile(y_pdf_samples, q=5, axis=0)
y_pdf_upp = jnp.percentile(y_pdf_samples, q=95, axis=0)
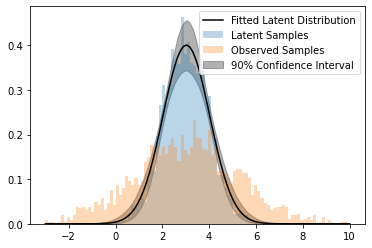
plt.hist(y_latent, bins=x, alpha=0.3, density=True, label="Latent Samples")
plt.hist(y, bins=x, alpha=0.3, density=True, label="Observed Samples")
plt.plot(x, y_pdf, color="k", label="Fitted Latent Distribution")
plt.fill_between(x, y_pdf_low, y_pdf_upp, color="k", label="90% Confidence Interval", alpha=0.3)
plt.legend()
plt.show()
Method = simple, Perf = -4459.04141604972
Method = importance, Perf = -4459.056578949637
**Best Method = simple**